
Oil & Gas Journal, 94:18, 4/29/1996
Alexander Aynbinder, Boris Taksa
Gulf Interstate Engineering Houston
Methods for determining pipeline wall have been developed which may reduce the required thickness by up to 7%, depending on steel grade and required design pressure.
A more precise calculation for pipeline wall can yield significant savings since costs of cross country pipelines are greatly affected by the quantity of required steel. This quantity is a function of line pipe length and wall thickness.
Existing methods for calculating wall thickness are debated among numerous engineers. A recent analysis of published methods concluded that wall-thickness design formulations should be improved.1
Gulf Interstate Engineering Co. has studied these formulations and prepared analytical solutions to calculating pipeline wall thicknesses under the influence of ratio of diameter and wall thickness, distribution of stresses across the pipe wall, and nonlinear property of pipe material.
The present discussion evaluates stress analysis of steel pipe resulting from both internal and external pressures. This analysis does not apply where external pressure may cause collapse.
For the purpose of analysis, the pipe is modeled as a long cylindrical shell or annulus consisting of a material with nonlinear properties. The results of calculating the wall thickness or maximum design pressure using this method are compared with traditional linear formulation as detailed in ASME B31.4 and B31.8.2 3
The solutions for determining wall thickness proposed here account for stress distribution across the pipe wall and the nonlinear material properties of the pipe. They also use the basic principle and methodology of ASME B31.4 and B31.8 standards and, therefore, may be used in design practice.
The first simple analytical solution in determining hoop stress due to internal pressure assumes that pipe wall thickness is so small that the outside radius is equal to the inside radius of the pipe and that hoop stress distribution is constant across the wall.
Then from a static condition of equilibrium, the hoop stress is determined by Equation 1 (see equations box).
For this assumption, the radial stress value is equal to internal pressure value, and the Tresca combined (equivalent) stress is determined by Equation 2.
Assuming that the combined stress is equal to allowable stress value (Sal), the allowable internal pressure from Equation 2 is determined according to Equation 3. This equation has qualitative agreement with equations in the Codes,2 3 paragraphs 404.1.2 and 841.11, respectively.
The second analytical solution for linear material considers the distribution of hoop and radial stresses across the wall, known as the Lame' solution.4 These stresses are calculated by Equations 4 and 5.
The average hoop stress for this solution is determined by Equation 6. Tresca combined stress, using average hoop stress and maximum radial stress, for case pe = 0 is defined by Equation 7.
With the assumption that the above combined stress is equal to the allowable stress, then Equation 7 as well as Equation 3 have qualitative agreement with the Codes' equations, paragraphs 404.1.2 and 841.11, previously cited.
Distribution of hoop and radial stresses across the wall, described by Equations 4 and 5, shows that the maximum hoop and combined stress take place on the inner surface, but it is known that the bursting of pipe due to internal pressure starts from an external wall surface.
These solutions and equations were obtained by use of linear, elastic models of steel pipe. This means that for the pipe steel's stress-strain diagram, the stress is always proportional to strain.
The actual stress-strain diagram has a limit of proportionality. After that limit point is reached, the slope of the curve changes as has been shown elsewhere (OGJ, Feb. 20, 1995, p. 70).
When the internal pressure is increased to greater than the value (that produces the maximum combined stress on the inner surface of pipe) equal to the proportionality limit, the area of the wall nearest the inner surface is in a plastic condition.
Designate this area as rp. It is understood that always ri < rp < ro.
In general, we have plastic and elastic areas: in rp= ri, the maximum combined stress reaches the proportional limit at the inner surface and the whole area of a wall is elastic; in rp= ro, the entire wall is plastic.
For design purposes, we will use an elastic, linearly hardening stress-strain diagram, which is simpler and more conservative than actual stress-strain diagrams. In the plastic and elastic areas, Equation 8 represents the combined stress-strain diagram.
Because of internal and external pressure on a pipe annulus, the equation from static condition of equilibrium4 and Tresca combined stress are defined by Equations 9 and 10, respectively.
Based on this model, a solution for both plastic and elastic areas can be found.
Assuming that the distribution of combined strain is inversely proportional to the square of the radius (Equation 11) and the strain along the boundary between elastic and plastic area (r = rp) is defined by Equation 12, Coefficient A can be determined.
The distribution of combined strain is then calculated by Equation 13. Considering Equation 13, the first expression in Equation 8 may be rewritten as Equation 14.
Considering Equation 10 and by substitution of Equation 14 into Equation 9, the differential equation for plastic area may be written as Equation 15.
Solution of Equation 15 gives the distribution of radial stress which is determined per Equation 16.
Distribution of hoop stress in the plastic area of the wall (ri < r < rp), using Equations 10, 14, and 16, is determined by Equation 17.
Constant (C) in Equations 16 and 17 is determined from boundary condition shown in Equation 18. Then, from Equations 16 and 17, the distribution of radial and hoop stresses in the plastic area (ri < r < rp) of a wall can be written as Equations 19 and 20.
Distribution of combined stress in the plastic area (ri < r < rp) of the wall according to Equations 10, 19, and 20 is determined by Equation 21.
In the elastic area (rp < r <ro), the equation of static equilibrium will be the same as Equation 9. This differential equation may be rewritten, relative to radial movement u using Hook's law5 and the relationship between strain and movement in radial direction, as Equation 22.
The solution for this differential equation written in movement or in stresses is given by Equations 23 and 24, respectively. Two constants (C1 and C2) are determined from boundary conditions according to Equation 25.
Substituting the values of constants in Equation 24, Equations 26 and 27 yield the distribution of radial and hoop stresses in the elastic area (rp < r < ro).
The value of pressure which produces plastic strain in the area between ri and rpcan be determined from the equality of the radial stresses for point r = rp, according to Equations 19 and 26.
Then, the value of pressure can be found with Equation 28.
If the value of plastic area radius rpis known, then the pressure may be determined from Equation 28, and the distribution of hoop stress may be found with Equations 20 and 27.

Fig. 1 [66072 bytes]shows distribution of the hoop stress vs. the plastic zone radius for case pe = 0. The input data are presented in this figure, and calculations assume that proportional limit is equal to 70% of yield strength.
The hoop stress reaches the maximum on the boundary between the plastic and elastic areas and, when an entire pipe wall is in plastic condition, the maximum hoop stress is on an external surface.
The maximum pressure is determined from Equation 28 from the condition at which the elastic radius (rp) reaches the value of an outside radius (ro). This pressure is calculated by Equation 29.
The distribution of hoop stress corresponding to this pressure is determined by Equation 30, which was obtained from Equation 20. According to Equation 30, the maximum hoop stress is on the external wall surface for case pe = 0.
These results take into account the non-linear property of the pipe material and are in qualitative agreement with experiments, which show that bursting of pipe from internal pressure starts at the external surface of the pipe wall.
Taking into account the principles presented in the codes2 3 that the maximum hoop stress should equal the allowable stress and modifying Equation 29, Equation 31 was obtained. This equation links design pressure, nominal wall thickness, nominal outside diameter, and allowable hoop stress.
Equation 31 can be used for calculating the design pressure or the design nominal wall thickness.
Equation 32 for calculating hardening modulus is based on the assumption that stress limit proportionality is equal to 70% of yield strength and the linear hardening lasts up to the yield strength. The value of specific minimum yield strength and the strain required to produce this strength is defined by such pipe specifications as, for example, API 5L.6
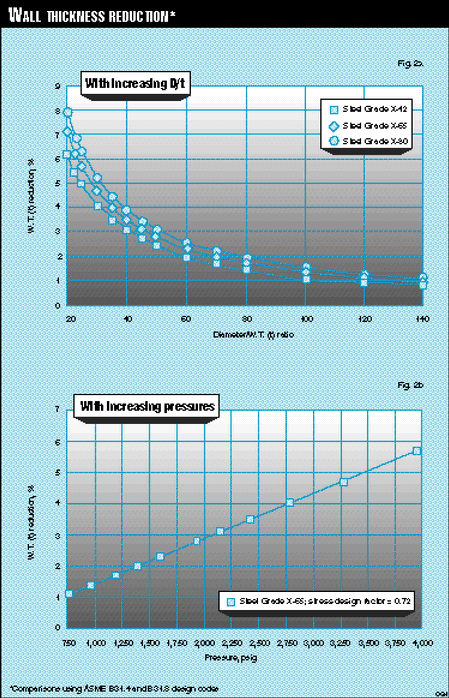
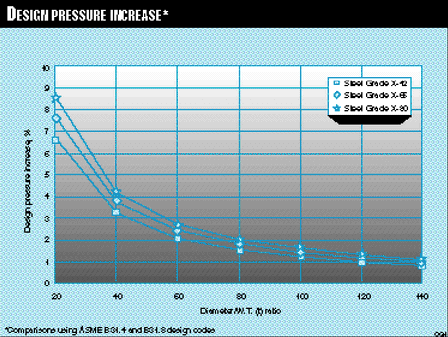
Figs. 2 [142331 bytes] and 3 [64467 bytes] present a comparison of results calculated by the subject equations and equations in the codes.
In Fig. 2, the axes "W.T. reduction, %" reflect wall thicknesses calculated with the new equations incorporated into current design codes less wall thicknesses calculated without, divided by wall thicknesses calculated without the new equations incorporated into the design codes.
Similarly, in Fig. 3, the axis "Increase in design pressure, %" reflects design pressures calculated with the new equations incorporated into current design codes less design pressures calculated without incorporating the new equations, divided by the design pressures calculated without incorporating the new equations into the codes.
The new equations provide a more economical solution.
For a high-pressure pipeline, these equations may save up to 5% of the required steel, and for common design pressure pipelines, savings of up to 1.5% of steel may be realized.
The next subject relates to hoop-stress design factor. The design factor considers dimensional tolerance, failure statistic of pipelines, probability, and cost of rehabilitation and public safety. In this article we consider only underthickness tolerance.
ASME B31.4 as well as B31.8 note that "in setting the values of a design factor, due consideration has been given and allowance has been made for the various underthickness tolerances provided for in pipe specification listed and approved for usage in code."
For example, according to API 5L for pipe grades X-42 through X-80 and for pipe diameters less than 20 in., the maximum underthickness tolerance is 12.5%; for welded pipe diameter 20 in. and larger maximum, 8%.
However, existing pipe manufacturing technology may guarantee underthickness tolerance of 4-5%. Considering this actual tolerance, which can be requested in material specifications for pipe manufacturing, the allowable nominal wall thickness may be reduced.
Assuming that the allowable pressure is proportional to minimum wall thickness (nominal thickness less underthickness tolerance), as in foreign codes,7-9 then if guaranteed underthickness tolerance is less than the codes specify, the design factor may be increased and calculated as shown in Equation 33.
Using ASME B31.4 for pipe wall calculations, the applicable allowable hoop stress may be calculated by equation paragraph 402.3.1, in which the value of 0.72 should be exchanged by a value obtained in Equation 33, where F = 0.72.
Using ASME B31.8 for pipe wall calculations, the applicable allowable hoop stress may be calculated according to Equation 34.
Traditional calculations for determining pipe wall thickness or design pressure formulation that are being used in current design codes2 3 fail to describe completely the relationship between stresses, pressure, diameter, and wall thickness. These formulas may be improved by considering the distribution of stresses across the pipe wall and the nonlinear property of pipe steel.
Methods described here take into account the distribution of stresses, nonlinear property of pipe steel, and the main principle and methodology of the codes, and may therefore be safely used in the design of the pipe wall thickness or pressure.
These equations allow more accurate determination of allowable wall thickness which may result in a reduction of up to 7% in wall thickness.
A sample calculation using the equations for the design of the pipeline wall thickness is also presented in Table 1 [33532 bytes].
The analysis here gives some rigorous bases for consideration to modify the codes for pipeline design which will safely reduce the required pipe wall thickness.
1. Verley, R., Lund, S., Moshagen, H., "Wall Thickness design for high pressure offshore gas pipelines," 1994 OMAE, Vol. V, Pipeline Technology ASME 1994, pp. 93-100.
2. ASME B31.4-94, "Liquid Transportation Systems for Hydrocarbons, Liquid Petroleum Gas, Anhydrous Ammonia, and Alcohols."
3. ASME B31.8-94, "Gas Transmission and Distribution Piping Systems."
4. Timoshenko, S., Strength of materials, 3rd Edition. Part II. New York: Kriegas, Huntington, 1976.
5. Desai, C., Abel, J., "Introduction to the finite element method," Van Nostrand Reinhold Co.
6. API Spec 5L-95, "Specification for Line Pipe."
7. BS 8010; Part 3, 1993, British Standard, "Code of Practice for Pipelines, Part 3, Pipelines Subsea: Design, Construction and Installation."
8. ISO TC 67 SC2, Draft of the International Organization for Standardization, "Pipeline Transportation Systems for the Petroleum and Natural Gas Industries."
9. NEN 3650- 1992, Dutch Standard, "Requirements for Steel Pipeline Transportation Systems."

Boris Taksa is vice-president of Gulf Interstate Engineering, responsible for development of business in Eastern Europe and the former Soviet Union. He joined GIE in 1979.
Before immigrating to the U.S., Taksa worked at the State Research Natural Gas Institute in Moscow after graduating from the Moscow Institute for the Petrochemical & Gas Industry. He is a member of the ASME B31.8 Code committee.

Alexander Aynbinder is a senior principal engineer in Gulf Interstate Engineering's civil engineering department in Houston. Before immigrating to the U.S., he was a lead research scientist in the former Soviet Union's State Research Institute for Pipeline Construction.
Aynbinder is a graduate of the Moscow Civil Engineering Institute and received a PhD in civil engineering from the Central Research Institute of Civil Structures in Moscow.
Copyright 1996 Oil & Gas Journal. All Rights Reserved.