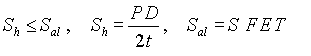 (1)
(1)Proposal to Modify ASME Code B31.8
Wall Thickness/ Pressure
Determination
Alexander Aynbinder, Fluor Daniel Inc.
Boris Taksa, Gulf
Interstate Engineering
Over the past several years, design criteria and equations for determining required line pipe wall thickness have become an important issue with oil and gas transportation companies. Safety records of the pipeline operating companies and published results of experimental and analytical studies indicate that the present traditional design formulation is conservative. Modification of this conservative bias is possible and will enable pipeline companies to reduce pipeline wall thickness without compromising the integrity of a new pipeline.
The existing method of calculating the required wall thickness or allowable pressure as presented in ASME Code B31.8 is based upon the allowable hoop stress. B31.8, Para. 805.234 states that "the maximum allowable hoop stress is the maximum hoop stress permitted by this Code for the design of a piping system."
The B31.8 variables for determining wall thickness/design pressure and the corresponding equations for calculating hoop stress and allowable hoop stress are:
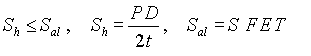 (1)
(1)
where
Sh
= hoop stress
Sal = allowable hoop stress
P =
design pressure, which is the maximum pressure permitted by the Code
D
= nominal outside diameter of pipe
t = nominal wall
thickness
S = specified minimum yield strength
F =design
factor which depends upon type of facilities and location class
E =
longitudinal joint factor
T = temperature derating factor.
B31.8 does not include any criteria or equations for modifying the wall thickness due to the combined effects of temperature rise and internal pressure for restrained onshore pipelines.
This proposal to modify B31.8 consists of three parts:
1.
Consideration of the minimum wall thickness (design factor)
2. A precise
equation for hoop stress determination
3. The consideration of wall thickness
versus temperature differential for a restrained pipeline
The proposed method uses the basic principles and methodology of B31.8 and the concept of limit state design [1].
The allowable hoop stress per B31.8 is a percentage of the
specified minimum yield strength (SMYS)ß
ß As
pointed out in the SUPERB study1 the SMYS may be used as criterion
for allowable hoop stress if the yield to ultimate stress ratio is not higher
than 0.9.
that and is determined by and depends upon a design factor. The design factor is a very complicated parameter [2]. The design factor should consider failure statistics of pipelines, the probability of a specified property of the material, the cost of rehabilitation, public safety, and dimensional tolerances. Special studies and evaluations require changing these values for different conditions.
ASME Code B31.4 [3] as well as B31.8, Para. 841.11 note that "In setting the values of the design factor, due consideration has been given and allowance has been made for the various underthickness tolerances provided for in the pipe specifications listed and approved for usage in this Code."
We will examine the question of minimum wall thickness or/and underthickness tolerance, which is part of the design factor.
According to API Specification 5L [4], for a pipe diameter of less than 20 inches, the maximum negative tolerance is -12.5% of the specified nominal wall thickness; for Grade X42 or higher welded pipe with a diameter of 20 inches and larger the maximum negative tolerance is -8.0% of the specified nominal wall thickness.
However, existing pipe manufacturing technology may is able to produce pipe with a guaranteed negative tolerance with an absolute value that is less than that specified by the Code. In fact, guaranteed negative tolerances with an absolute value of less than 5% of the nominal wall thickness are often encountered. If one takes into account the actual tolerance, which can now be requested in material specifications for the manufacture of pipe for a specific project, the allowable or required nominal wall thickness may be reduced.
Assuming that the allowable pressure is proportional to the minimum wall thickness (nominal thickness minus the underthickness tolerance), as in some foreign codes,, then if the absolute value of the guaranteed negative tolerance is less than that specified by the codes, the design factor can be increased and would be calculated by the following equation
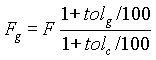 (2)
(2)
where
Fg = proposed design
factor
tolg = absolute value of the guaranteed (specified)
negative tolerance, % (negative value)
tolc = absolute
value of the negative tolerance approved by codes, % (negative value).
Using the B31.8 criteria for pipe wall thickness calculations, the applicable allowable hoop stress is calculated by the equation
![]() (3)
(3)
As an example therefore, using equations (2) and (3) above, for pipe having a guaranteed negative tolerance of -5%, the allowable hoop stress could be increased, and therefore the nominal wall thickness could be decreased by: as shown in the table below:
|
Pipe Diameter |
Allowable Hoop stress increase |
| < 20 inches (Welded or seamless) |
8.5% |
| >= 20 inches (welded) |
3.2% |
| >= 20 inches (seamless) |
5.5% |
B31.8 uses Barlow’s formula for hoop stress determination. This formula is based upon the assumptions that a) the hoop stress across the pipe wall is constant, b) the section of pipe is a ring with a diameter equal to the nominal outside diameter, and c) the distribution of radial stresses across the wall is neglected. The hoop force in a ring is defined from the static condition of equilibrium and hoop stress is calculated for the nominal wall thickness.
Next, the more complicated analytical solution for linear elastic material considers the distribution of hoop and radial stresses across the wall and is known as the Lame Solution. It should be particularly emphasized that per the Lame solution, the maximum hoop stress due to internal pressure occurs on the inner wall surface, but it is known that the bursting of a pipe due to internal pressure starts from an external wall surface.
The trend of the pipeline codes is to permit designs based upon limit-state criteria [1]. One of the conservative methods for limit-state design is to apply traditional allowable stress criteria for calculated stresses while considering the actual, nonlinear behavior of the material.
The proposed wall thickness/design formulation [8] considers the nonlinear property of pipe material, i.e. the elastic-plastic stress-strain diagram. This method allows a very simple determination not only of the stress but also of the corresponding strain and utilizes, if required, the allowable strain criterion. The proposed formulation also considers the distribution of radial stress across the wall. B31.8 has no limitation on internal pressure, so in some cases radial stress can be significant, and its role in determining pipe-wall thickness cannot be neglected.
As is known from the Lame Solution, in the elastic range of stress the maximum hoop stress and combined stress due to internal pressure take place on the internal surface. With internal pressure being increased above the value that produces combined stress on the inner surface of pipe equal to the proportional limit, the area of the wall nearest the inner surface is in a plastic condition.
The stress-strain diagram in elastic and plastic areas shall be described. The stress-strain diagram has a limit of proportionality. After that limit point is reached the slope of curve changes and can be described in different ways [9]. We will designate the first area as the elastic area; the second will be designated as the plastic area.
An elastic, linear hardening stress-strain diagram (showing the relationship between combined stress and combined strain) is being used for the pipeline wall thickness required due to pressure. This diagram is conservative in this case and results in a simplified analytical solution for design purposes. It was assumed that the elastic area isranges from zero to the stress of proportionality limit with and has a tangent equal to the modulus of elasticity. The limit of proportionality between stress and strain is approximately equal to 70 – 75% of the yield stress. The proposed equation for calculating the hardening modulus is based upon the assumption that the stress limit proportionality Sp is equal to 72% of the yield strength and linear hardening lasts up to the yield stress
![]() (4)
(4)
where
Eo = modulus of
elasticity
eys = strain corresponding to the yield stress
(0.005 for API 5L pipe).
The distribution of the hoop stress due to internal pressure in the elastic and plastic areas and the corresponding pressure that produces these stresses was were obtainedß
based upon the differential equation of equilibrium for the annulus, boundary conditions, and elastic linear hardening stress-strain diagram.
The distribution of the hoop stress in the elastic and plastic areas of the pipe wall and the internal pressure that produces these stresses are determined by equations
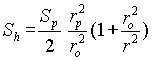 (5)
(5)
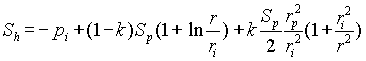 (6)
(6)
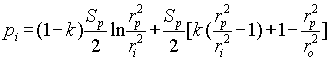 (7)
(7)
where
ri = inside radius of
pipe
ro = outside radius of pipe
rp
= plastic zone radius
k = Eh /
Eo = ratio of hardening modulus to elastic
modulus
Sp =limit of proportionality.
Figure 1 shows the distribution of hoop stress in the entire wall area due to internal pressure versus the plastic zone radius (PZR) in 42" x 0.625" pipe (Sp =46.8 ksi, S = 65 ksi).
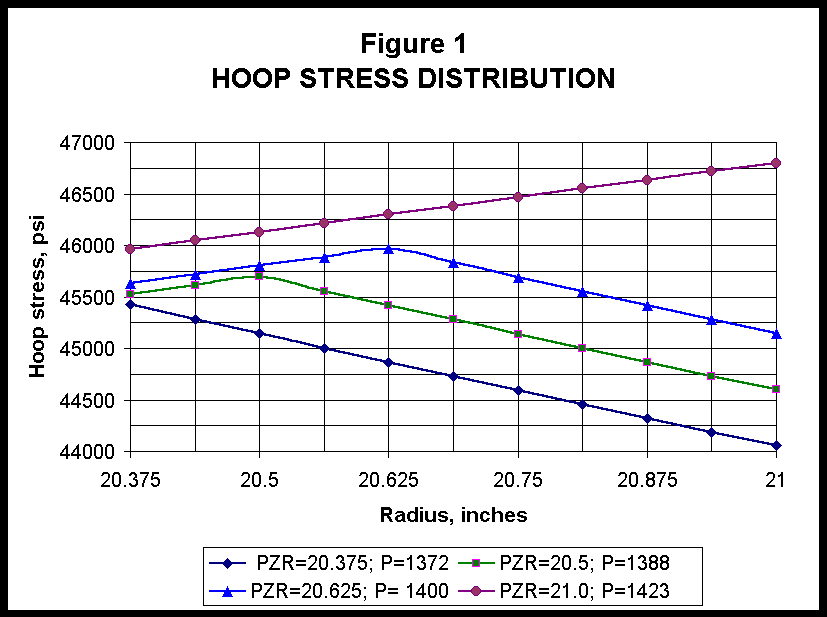
The lower line represents the solution for the case when the plastic zone radius is equal to an inside radius, i.e. an elastic linear solution that agrees with the well-known Lame Solution. For the linear model of steel, the maximum hoop stress is on the inner surface of the pipe wall.
As part of the pipe wall is in a plastic condition, the hoop stress reaches the maximum on the boundary between the elastic and the plastic areas.
The upper line represents the solution for the case when the plastic zone radius is equal to an outside radius; i.e. the entire pipe wall is in a plastic condition. The hoop stress reaches the maximum on the external surface. This latter solution is in qualitative agreement with the experiments that demonstrate that the bursting of pipe from internal pressure starts on the external surface of the pipe wall.
Based upon equations (5), (6) and (7), the maximum hoop stress, which occurs on the external surface of the pipe, versus pressure and pipe size is
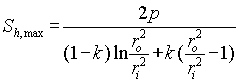 (8)
(8)
According to B31.8, the maximum allowable hoop stress is the maximum hoop stress permitted by the Code for the design of a piping system. To comply with Code requirements, the allowable design pressure versus allowable hoop stress may be calculated as
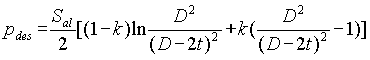 (9)
(9)
This equation links the design pressure with the nominal wall thickness, the nominal diameter and the allowable hoop stress, and enables one to determine the required nominal wall thickness for an established operating pressure.
Equation (9) takes into account the distribution of hoop and radial stresses across the pipe wall, the nonlinear property of pipe steel and the main principals and methodology of the Code. The hoop stress determination is based upon limit state concepts and design pressure determination is based upon the traditional method utilizing allowable hoop stress.
Assume that the hardening modulus is equal to zero, i.e., the nonlinear property of steel is described by an elastic, idealized plastic stress-strain "Prandtl Diagram". In this case k = 0 and equation (9) is in qualitative agreement with equation (35a) in paragraph K304.1.2 of ASME B31.3 [10], which is used for calculating the wall thickness of straight pipe under high internal pressure. Equation (9) is also in agreement with the second equation in paragraph AD-201 of ASME Section VIII, Division 2 [11], which is used for calculating the wall thickness of cylindrical shells.
The table below shows the percentage increase in value obtained by calculating the design pressure from the equations proposed above vs. B31.8 equations, using the same allowable stress for grade X-65 steel.
|
D/t |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
100 |
|
Pd/Pcode, % |
7.7 |
5.0 |
3.7 |
2.9 |
2.4 |
2.1 |
1.8 |
1.4 |
The proposed method of hoop stress determination therefore provides a more economical solution.
For a restrained pipeline, determining wall thickness versus temperature differential is important for modern pipelines. Increased wall thickness may be required or it could be necessary to cool the transported product. Also, pipelines being constructed in Arctic regions may require increased wall thickness due to the combined effects of temperature rise and pressure.
Unlike B31.4, B31.8 does not include criteria for longitudinal stress and equivalent (combined) stresses and does not include an equation for determining the longitudinal stress for a restrained pipeline. In our opinion these, factors should be incorporated into B31.8.
In B31.8, it is proposed to include the criteria of longitudinal stress and the equivalent (combined) stress based upon Von Mise’s theories for onshore restrained pipelines. This is similar to the criteria for offshore pipelines in B31.8.
![]()
![]() (10)
(10)
![]()
![]() (11)
(11)
where
Sh = hoop
stress
SL = axial longitudinal stress, sign positive at
tensile stress
S = specified minimum yield stress.
There is every reason to consider the nonlinear property stating that the allowable stress of 90% SMYS exceeds the proportionality limit of the steel. For example, for the linear model the strain corresponding to a stress of 90% SMYS for steel of grade X-52 is approximately 0.17%, and the actual strain that produces this stress is approximately 0.26%. It can therefore be seen that the actual strain is over 50% greater than that given by the linear model.
The axial longitudinal tensile stress is determined by the generalized Hook’s law for restrained conditions and should be based upon the effective Young’s modulus and the effective Poisson’s ratio
![]() (12)
(12)
where
SL = axial longitudinal tensile
stress
Sh = hoop stress due to pressure, may be calculated
by Barlow’s equation
T1 = temperature at time of
installation
T2 = maximum or minimum operating
temperature
a = linear coefficient of thermal
expansion
Eef = effective Young’s
modulus
vef = effective Poisson’s ratio.
In this modified classical equation the elastic modulus and Poisson’s ratio are replaced with the effective Young’s modulus and the effective Poisson’s ratio, which consider the nonlinear property of the pipe material. This modification is based upon the theory of small elastic-plastic strains.
The effective Young’s modulus is the secant modulus determined per the uniaxial stress-strain diagram
![]() (13)
(13)
where
Sa = actual equivalent (combined)
stress calculated per equation (10) and (11). For wall
thickness/allowable temperature differential determinations this value is equal
to 0.9S
eas = the strain that produces the stress equal to
Sa, which is determined in accordance with the uniaxial
stress-strain diagram for pipeline steelß
See Appendix
for Guideline
In accordance with the theory of small elastic-plastic strains, the effective Poisson’s ratio is calculated as
![]() (14)
(14)
where
Eo = modulus of
elasticity
vo = Poisson’s ratio
Eef =
effective Young’s modulus
The proposed method [8] will consider the nonlinear property of pipe steel and can be used to accomplish the following three tasks:
Below are the results of calculations for a restrained 24-inch pipeline, grade X-52, with a design pressure of 1440 psig:
Thus, for a restrained pipeline the suggested method essentially permits an increase in the allowable temperature differential (cooling temperature) or a reduction of the required wall thickness
Code Consideration:
The analysis below gives a rigorous basis for the proposal to modify ASME B31.8. Acceptance of the proposal will safely reduce the required wall thickness.
The formula for design pressure/wall thickness determination:
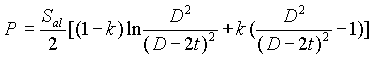
![]()
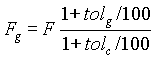
![]()
where (in addition to the Code
definitions):
Fg = proposed design
factor
tolg = guaranteed (specified) negative pipe
tolerance, % (negative value)
tolc = negative pipe
tolerance approved for usage in this code, % (negative
value)
eys = strain that produces the yield stress (0.005
for API 5L pipe)
Eo = modulus of elasticity
k =
ratio of the hardening modulus to the elastic modulus.
Restrained Pipelines
Longitudinal and combined (equivalent) stresses for restrained pipelines shall not exceed values found from
![]()
![]()
![]()
![]()
The axial longitudinal tensile stress due to the combined effects of temperature rise and internal pressure shall be computed from the equations
![]()
where
SL = axial longitudinal tensile
stress
Sh = hoop stress due to pressure, per
805.233
T2 = maximum or minimum operating
temperature
T1 = temperature at time of
installation
a = linear coefficient of thermal
expansion
Eef = effective Young’s
modulus
vef = effective Poisson’s ratio.
The effective Young’s modulus is the secant modulus determined per uniaxial stress-strain diagram
![]()
where
Sa = actual equivalent (combined)
stress. For the determination of the wall thickness/allowable temperature
differential, this value is equal to 0.9S (90% of SMYS)
ea
= the strain that produces the stress equal to Sa,
which is determined in accordance with the uniaxial stress-strain diagram for
pipeline steel (see guidelines).
The effective Poisson’s ratio in accordance with the theory of small elastic-plastic strains is calculated as
![]()
where
Eo = modulus of
elasticity
vo = Poisson’s ratio
Eef =
effective Young’s modulus.
We hope that this proposal for Code modifications will be useful for pipeline design.
APPENDIX
1. Hoop stress distribution
An elastic, linear hardening stress-strain diagram (showing the relationship between combined stress and combined strain) is being used for wall thickness calculation due to pressure. This diagram is conservative in this case and results in a simplified analytical solution for design purposes.
It was assumed that the elastic area is up to ranges from zero to the stress of proportionality limit with a tangent equal to the modulus of elasticity. The range of the plastic area is from the limit proportionality up to the yield stress with a tangent equal to the modulus of hardening.
The combined stress-strain diagram (the relationship between the Tresca combined stress Sc and combined strain ec) may be represented by the equation
![]() (A1)
(A1)
![]()
![]() (A2)
(A2)
where
Eo = modulus of
elasticity
Eh = hardening modulus
Sp =
proportional limit of diagram.
Considering hoop and radial stresses, the Tresca combined stress for pipe due to internal pressure is
![]() (A3)
(A3)
Assuming that the distribution of combined strain is inversely proportional to the square of the radius
![]() (A4)
(A4)
Then, from the boundary condition between elastic and plastic areas
![]() (A5)
(A5)
the distribution of combined of strain and stress is
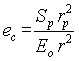 (A6)
(A6)
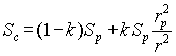 (A7)
(A7)
The ratio of the hardening modulus to the elastic modulus is designated as
![]()
![]() (A8)
(A8)
The differential equation from the static condition of equilibrium for an annulus due to internal pressure is
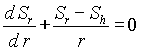 (A9)
(A9)
Considering equation (A3) and (A8) and by substitution of equation (A7) into equation (A9) the differential equation for a plastic area may be written as
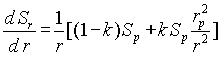 (A10)
(A10)
The solution of equation (A10) gives the distribution of radial stress in a plastic area
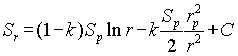 (A11)
(A11)
Based upon the above solution (A11), the distribution of hoop stress is![]()
![]()
 (A12)
(A12)
The constant ‘C’ in equation (A11) and (A12) is determined from the boundary condition on the inside of the pipe wall
![]() (A13)
(A13)
Then, from equation (A11) and (A12), the distribution of radial and hoop stresses in a plastic area of can be written
 (A14)
(A14)
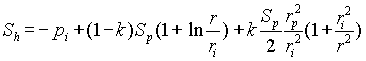 (A15)
(A15)
Substituting equations (A14) and (A15) into equation (A3), the distribution of combined stress is
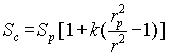 (A16)
(A16)
So, the equation (A14) – (A16) gives the distribution of both components of stress and Tresca combined stress.
Next, we must obtain the distribution of stresses in the elastic region of the pipe. In the elastic area the equation of static equilibrium will be the same as equation (A9). This differential equation may be rewritten relative to radial movement u, using Hook’s law and the relationship between strain and movement in the radial direction7.
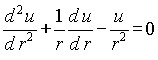 (A17)
(A17)
The solutions for the above of this differential equation, written insolved for movement or inand for stresses respectively, are as follows
![]() (A18)
(A18)
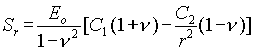 (A19)
(A19)
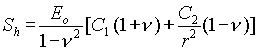 (A20)
(A20)
Two constants (C1 and C2) are determined from the boundary condition between elastic and plastic areas and the external wall of the surface, this condition being that the combined stress is equal to the limit proportionality between stress and strain and the radial stress is equal to the external pressure (zero).
![]() (A21)
(A21)
![]() (A22)
(A22)
Determining the values of constants and substituting them into (A19) and (A20), the final equations for radial and hoop stresses in elastic area are
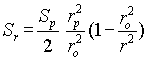 (A23)
(A23)
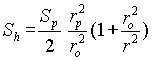 (A24)
(A24)
The value of pressure which produces plastic stress/strain can be determined from the equality of the radial stresses at the boundary of elastic and plastic areas, which is determined by equations (A14) and (A23).
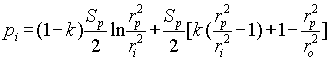 (A25)
(A25)
Equation (A25), which permits the determination of the internal pressure for a given radius of plastic area, is used to determine hoop stress distribution in the entire pipe wall area per equations (A24) and (A15) in the elastic and plastic areas, accordingly.
Based upon equations (A25) and (A15), the maximum hoop stress versus pressure and pipe size, which occurs on the external surface is
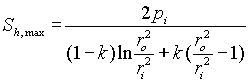 (A26)
(A26)
According to ASME B31.8, the maximum allowable hoop stress is the maximum hoop stress permitted by the Code for design of a piping system. To comply with Code requirements, the allowable design pressure versus allowable hoop stress may be calculated as
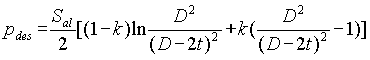 (A27)
(A27)
This equation links design pressure with nominal wall thickness, nominal diameter and allowable hoop stress, and allows the determination of the required nominal wall thickness for an established operating pressure.
The Equation (A27) takes into account the distribution of hoop and radial stresses across the pipe wall, the nonlinear property of pipe steel and main principals and methodology of the codes.
2. Guideline. Proposed stress-strain diagram
The proposed equations described uniaxial stress-strain diagram (S – e) for pipe steel (with the division of the stress-strain curve in three stress sections) and are based solely upon the available data presented in the Pipe Specs and the B31 Codes
![]()
![]()
![]()
where
![]()
![]()
![]()
![]()
Sys = specified minimum yield stress
(SMYS)
eys = strain corresponding to SMYS, = 0.005 per API
5L definition
Suts =specified minimum ultimate tensile
stress (SUTS)
euts = minimum elongation (strain) for
specimens with area of 0.20 sq. in.
Eo = modulus of
elasticity.
REFERENCES